The main aim here was to morph space inside a square but such that the transformation preserves some kind of ordering of the points. I wanted to use it to generate some random graphs on a flat surface and introduce spatial deformation to make the graphs more interesting.
I’ve got no idea how to do this - I suppose that the partial derivatives need to be all positive or negative. I believe that I’m after a homeomorphism but I’m out of my depth there… My initial attempt is described below.
I need a transformation \(\psi\) that maps from points inside a cube \([-1, 1] \times [-1, 1]\) to the same cube. The way I’ve tried to do it is by representing the transformation using a multi-output GP (where the outputs are independent). This GP is conditioned such that the border segments of the square are preserved.
\[X, Y \sim GP(0, k_{RBF})\] \[X, Y : \mathbb R^2 \mapsto \mathbb R\] \[\psi : (x, y) \mapsto (X(x, y), Y(x, y))\]All results below start with a uniform grid on a square as the one shown below.
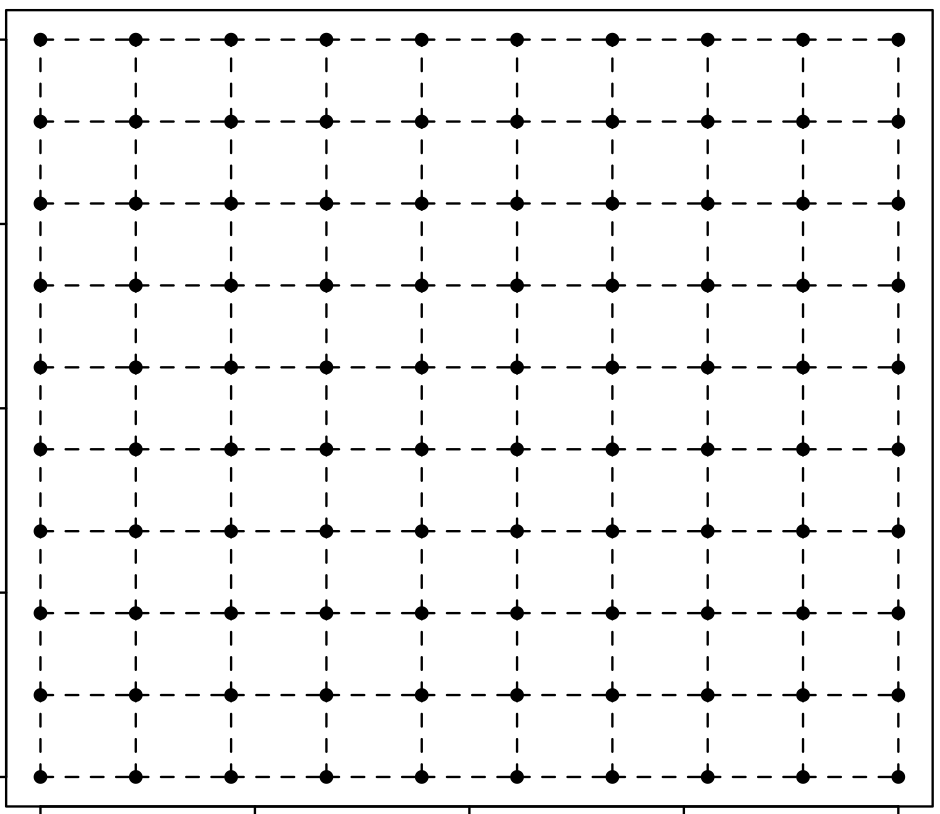
An example of a diffeomorphism
This example is from Wikipedia - I wrote an R implementation based on their (Mathematica?) one here.
R Code
library(data.table)
diffeo_example = function(n = 10, epsilon = 1.5) {
grid = data.table(expand.grid(x = seq(-1, 1, length.out = n),
y = seq(-1, 1, length.out = n)))
x = copy(grid$x); y = copy(grid$y)
A = 0.5 * epsilon * (0.25 * (cos(pi*x) + 1) *
(cos(pi*y) + 1) +
cos(0.5*pi*x) * cos(0.5*pi*y))
grid[, x_new := x - y*A]
grid[, y_new := y + x*A]
return(grid)
}
plot_results = function(grid, ...) {
grid[, plot(x_new, y_new, pch = 20, ...)]
grid[, {for(i in 2:.N) segments(x_new[i - 1], y_new[i - 1], x_new[i], y_new[i], lty = 2)}, by = y]
grid[, {for(i in 2:.N) segments(x_new[i - 1], y_new[i - 1], x_new[i], y_new[i], lty = 2)}, by = x]
}
plot_results(diffeo_example())Attempt
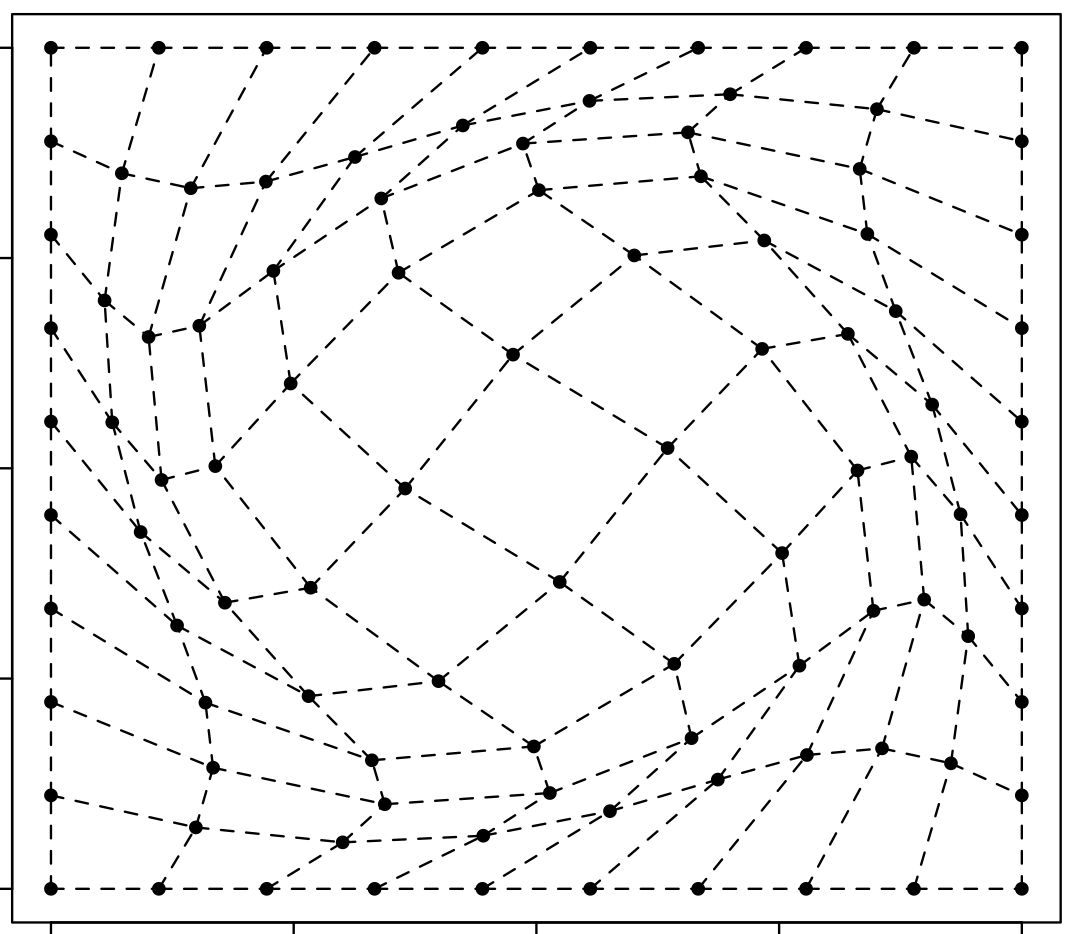
Below is some R code that simulates the formalisation above.

R Code
simulate_function <- function(v = 0.25, l = 0.5, n = 15, condition = 'x', enforce_grad_pos = T) {
grid = data.table(expand.grid(x = seq(-1, 1, length.out = n),
y = seq(-1, 1, length.out = n)))
x = copy(grid$x); y = copy(grid$y)
K_x = matrix(x, length(x), length(x), T) -
matrix(x, length(x), length(x), F)
K_x = v * exp(- K_x^2 / l^2)
K_y = matrix(y, length(y), length(y), T) -
matrix(y, length(y), length(y), F)
K_y = v * exp(- K_y^2 / l^2)
K = K_x*K_y
if(condition == 'x')
grid[(abs(y) == 1) | (abs(x) == 1), f_cond := x]
if(condition == 'y')
grid[(abs(y) == 1) | (abs(x) == 1), f_cond := y]
index_cond = grid[, which(!is.na(f_cond))]
index_unkn = grid[, which( is.na(f_cond))]
K11 = K[index_unkn, index_unkn]
K12 = K[index_unkn, index_cond]
K21 = K[index_cond, index_unkn]
K22 = K[index_cond, index_cond]
mu_bar = K12 %*% solve(K22 + diag(nrow(K22))*1e-10) %*% grid[index_cond, f_cond]
ch_bar = t(chol(K11 - K12 %*% solve(K22 + diag(nrow(K22))*1e-10) %*% K21 + diag(length(index_unkn))*1e-3))
setorder(grid, y, x) # this is a quick and dirty way of getting +ve grads
if(enforce_grad_pos & condition == 'x') {
grid[index_unkn, f_cond := mu_bar + ch_bar %*% rnorm(.N)]
while(grid[, diff(f_cond), by = y][, mean(V1 > 0) < 1]) {
grid[index_unkn, f_cond := mu_bar + ch_bar %*% rnorm(.N)]
}
}
if(enforce_grad_pos & condition == 'y') {
grid[index_unkn, f_cond := mu_bar + ch_bar %*% rnorm(.N)]
while(grid[, diff(f_cond), by = x][, mean(V1 > 0) < 1]) {
grid[index_unkn, f_cond := mu_bar + ch_bar %*% rnorm(.N)]
}
}
return(grid)
}
simulate_gp_results = function(v = 0.25, l = 0.5, n = 15) {
grid_x = simulate_function(n = n, v = v, l = l, condition = 'x')
setnames(grid_x, 'f_cond', 'x_new')
grid_y = simulate_function(n = n, v = v, l = l, condition = 'y')
setnames(grid_y, 'f_cond', 'y_new')
grid = merge(grid_x, grid_y, by = c('x', 'y'))
return(grid)
}
plot_results(simulate_gp_results(n = 15))Edit: it’d be nice to write up a script such that I can sample from the function conditioned on the gradients (easy to do with GPs as the derivative kernels are known analytically).
2021
Efficient Gaussian Process Computation
Using einsum for vectorizing matrix ops
Gaussian Processes in MGCV
I lay out the canonical GP interpretation of MGCV’s GAM parameters here. Prof. Wood updated the package with stationary GP smooths after a request. Running through the predict.gam source code in a debugger, the computation of predictions appears to be as follows:
Short Side Projects
Snowflake GP
Photogrammetry
I wanted to see how easy it was to do photogrammetry (create 3d models using photos) using PyTorch3D by Facebook AI Research.
Dead Code & Syntax Trees
This post was motivated by some R code that I came across (over a thousand lines of it) with a bunch of if-statements that were never called. I wanted an automatic way to get a minimal reproducing example of a test from this file. While reading about how to do this, I came across Dead Code Elimination, which kills unused and unreachable code and variables as an example.
2020
Astrophotography
I used to do a fair bit of astrophotography in university - it’s harder to find good skies now living in the city. Here are some of my old pictures. I’ve kept making rookie mistakes (too much ISO, not much exposure time, using a slow lens, bad stacking, …), for that I apologize!
Probabilistic PCA
I’ve been reading about PPCA, and this post summarizes my understanding of it. I took a lot of this from Pattern Recognition and Machine Learning by Bishop.
Spotify Data Exploration
The main objective of this post was just to write about my typical workflow and views. The structure of this data is also outside my immediate domain so I thought it’d be fun to write up a small diary working with the data.
Random Stuff
For dealing with road/city networks, refer to Geoff Boeing’s blog and his amazing python package OSMnx. Go to Shapely for manipulation of line segments and other objects in python, networkx for networks in python and igraph for networks in R.
Morphing with GPs
The main aim here was to morph space inside a square but such that the transformation preserves some kind of ordering of the points. I wanted to use it to generate some random graphs on a flat surface and introduce spatial deformation to make the graphs more interesting.
SEIR Models
The model is described on the Compartmental Models Wikipedia Page.
Speech Synthesis
The initial aim here was to model speech samples as realizations of a Gaussian process with some appropriate covariance function, by conditioning on the spectrogram. I fit a spectral mixture kernel to segments of audio data and concatenated the segments to obtain the full waveform.
Sparse Gaussian Process Example
Minimal Working Example
2019
An Ising-Like Model
… using Stan & HMC
Stochastic Bernoulli Probabilities
Consider:
